3차원에서 회전을 표현하는 방법

3차원 회전 표현의 어려움

2차원에서 각도를 표현함에 있어서는 큰 어려움이 없다. 굳이 어려움을 찾자면 부호에 따라 방향이 달라지는 것, 그리고 단위가 라디안인지 도(degree)인지를 확인하는 것 정도라고 할 수 있겠다. 그러나 3차원에서 3 자유도를 갖는 회전을 표현하는 것은 생각보다 쉽지 않다.

기준 축의 설정

먼저, 어떤 축을 기준으로 회전할 것인가가 첫번째 문제이다. 예를 들어, 아래와 같이 z축을 기준으로 \(\theta\) 만큼 회전하는 경우를 보자. z축을 기준으로 회전하고 나면 x축과 y축은 각각 x’, y’과 같이 변화하게 된다. 이 경우, z축으로 회전한 뒤, y축으로 회전하고 싶다면 변화 전 y축을 기준으로 회전해야 할까, 아니면 변화 후의 y’축을 기준으로 회전해야 할까?

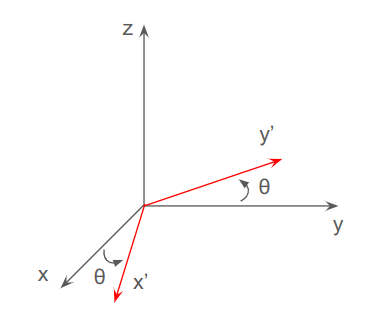
따로 정답이 있는 것은 아니고, 어떤 것을 선택하던지 일관되게 적용하면 된다. 변화하는 축을 기준으로 회전하는 것을 intrinsic rotation 이라 하고, 고정된 축을 기준으로 회전하는 것을 extrinsic rotation 이라 한다.

회전 순서의 중요성

회전 표현의 또 다른 어려움으로는 회전의 순서가 있다. 이동(translation)과는 달리, 회전에서는 순서가 바뀌면 결과가 달라진다. 즉, 교환법칙이 성립하지 않는다. 아래 그림은 intrinsic rotation으로 z축으로 90도 회전한 뒤, x축으로 90도 회전하는 경우와 x축으로 90도 회전한 뒤, z축으로 회전하는 경우를 비교한 그림이다. 색상 RGB가 축 XYZ에 대응된다(Red->X, Green->Y, Blue->Z).

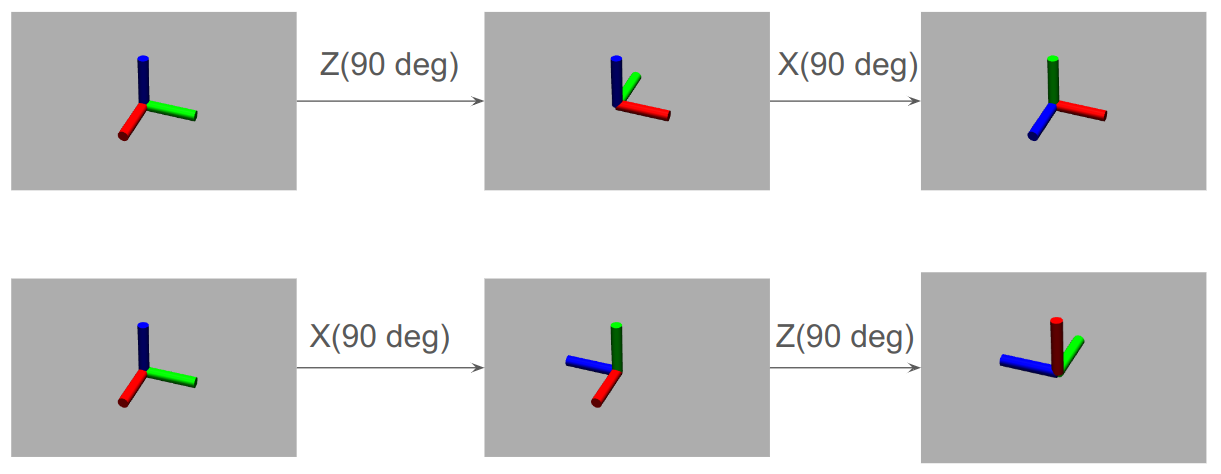
회전 순서에 따라 결과가 달라지는 것을 확인할 수 있다. 따라서, 이동의 경우처럼 단순히 회전 방향과 각도를 나열하는 것만으로는 정확히 회전을 표현할 수 없고, 회전의 순서도 반드시 함께 표기해주어야 한다.

3차원 회전의 표현 방법

이처럼 3자유도 회전을 표현하는 것은 이동에 비해 간단하지 않고, 따라서 이를 표현하는 방법에도 여러가지가 존재한다.

Roll-Pitch-Yaw

첫번째로 살펴볼 각도 표현방법은 RPY(Roll, Pitch, Yaw)라고 불리는 방법이다. 비행 쪽에서 많이 사용되는 방법이긴 하지만, 꼭 비행이 아니더라도 한 번 쯤은 들어봤을만큼 널리 쓰이는 방법 중 하나이다. 특별할 것은 없고, 아래 그림과 같이 x,y,z축 회전을 각각 roll, pitch, yaw 라는 이름으로 불러주는 것이고, 회전의 적용 순서는 intrinsic rotation의 경우 Y->P->R 이고, extrinsic rotation의 경우 R->P->Y 이다(왜 두 경우에 적용 순서가 달라지는 지는 Euler angle에서 설명한다). RPY 표현법은 다음에서 살펴볼 Euler angle의 하나의 예시이기도 하다.

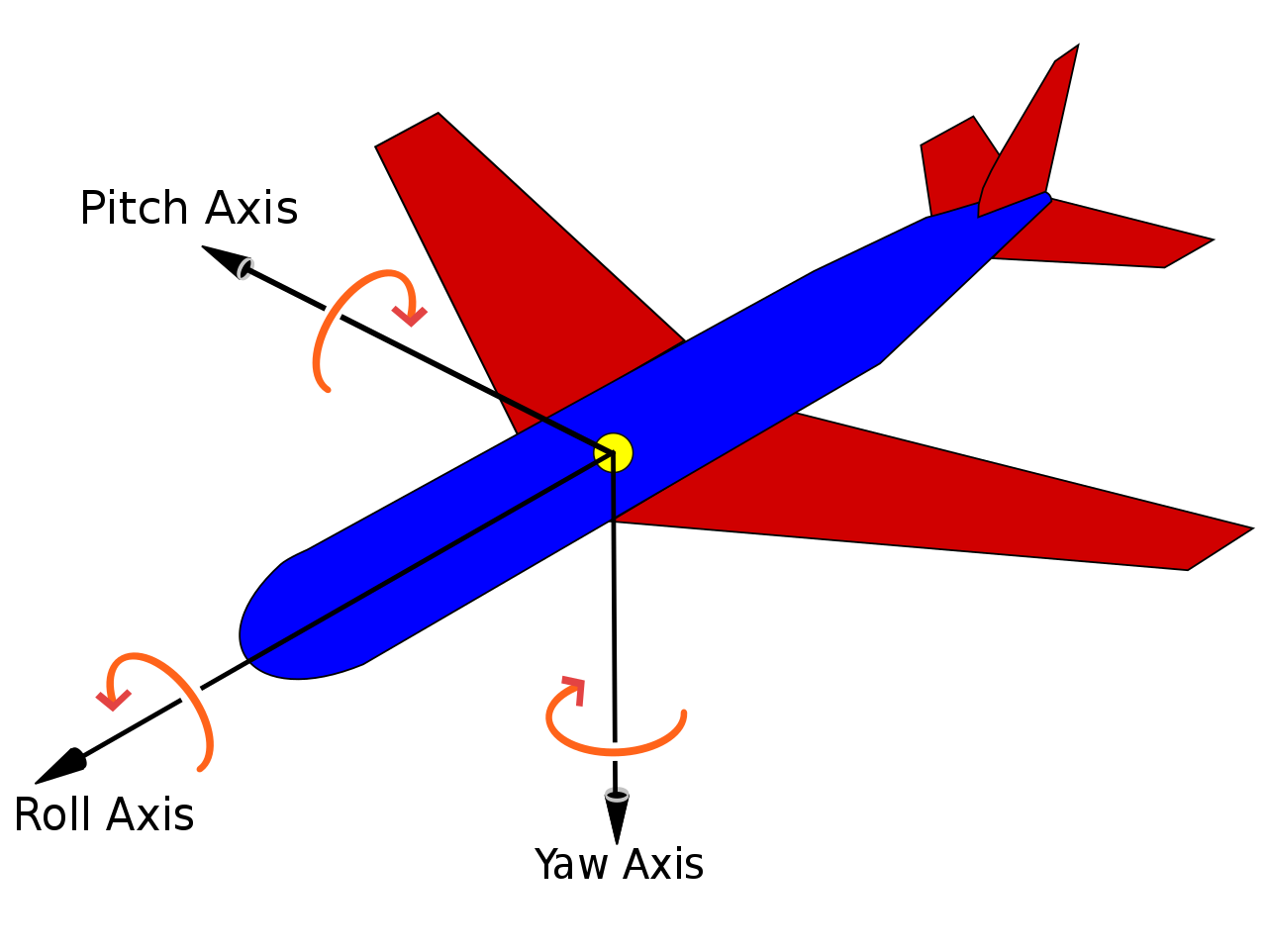By Yaw_Axis.svg: Auawisederivative work: Jrvz (talk) - Yaw_Axis.svg, CC BY-SA 3.0

Euler angle

Euler angle은 쉽게 말하자면, 가능한 회전의 순서를 모두 포함하는 것이라고 할 수 있겠다. 예를 들면, x,y,z축을 나열하는 방법은 총 6가지(x-y-z, x-z-y, y-x-z, y-z-x, z-x-y, z-y-x)가 있는데 각각이 Euler angle의 예시라고 할 수 있고, 이를 Euler xyz 또는 Euler zyx 와 같이 회전의 적용순서로 이름을 붙여 부르게 된다. 다만, 앞서 살펴봤던 것처럼 회전축을 결정하는 방법이 2가지(instrinsic, extrinsic)가 있으므로, 이를 별도로 표기해주는 것이 더 정확한 표현이라 할 수 있겠다(Euler angle의 정의를 보면 “고정된 축”으로 회전한다는 표현이 있기 때문에, 별도의 표기가 없다면 extrinsic으로 생각하는 것이 맞겠다).

여기서 재미있는 점은 사실 3개의 축이 모두 필요하지 않다는 점이다. 앞서 언급한 6가지 나열 방법 외에 2개의 축만을 이용하는 방법 6가지(x-y-x, x-z-x, y-x-y, y-z-y, z-x-z, z-y-z)가 추가로 존재한다. 이는 하나의 축으로 회전하게 되면 다른 축들의 방향이 변화하기 때문으로, 첫번째 회전하는 축과 세번째 회전하는 축이 이름은 같지만 회전할 때는 다른 방향으로 회전하게 되기 때문이다. 아래의 그림을 통해 이를 확인해보자.

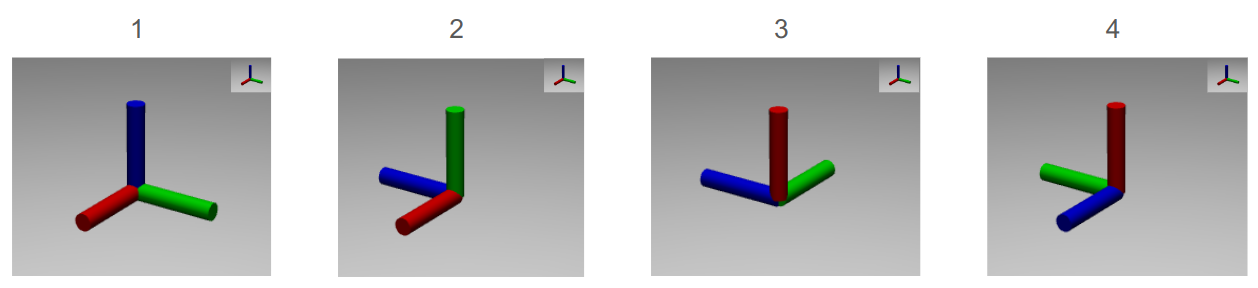
여기서 가운데 크게 나타나 있는 좌표계를 body frame 즉, 물체와 함께 회전하는 좌표계라고 하고, 우측 상단에 있는 좌표계를 fixed frame 즉, 회전하지 않는 좌표계라고 생각하자. 먼저, intrinsic rotation으로 위의 그림을 해석해보자. 1->2는 x축으로 90도 회전한 것이고, 2->3은 z축으로 90도 회전, 그리고 3->4는 x축으로 90도 회전한 것이다. 즉, intrinsic rotation으로 보면 x축과 z축 2개의 축으로만 회전한 것이다. 그러나 이를 extrinsic rotation으로 해석해보면 1->2는 x축 90도 회전, 2->3은 y축 -90도 회전, 그리고 3->4는 z축 90도 회전으로 이해할 수 있다. 즉, extrinsic rotation으로 보면 x,y,z 모든 축으로 회전한 것이다.

ℹ Info! extrinsic rotation의 경우, 축이 회전하지 않으니 첫번째 회전 축과 세번째 회전 축이 같은 것이 아닌가 생각할 수 있지만, 물체의 입장에서 보면 축이 회전한 것처럼 보이게 되므로 결국 같은 결과를 얻게 된다. 직접 한 번 물체를 회전해보며 생각해보길 권장한다.

이처럼 2개의 축을 이용하는 Euler angle은 로봇의 물리적 특성을 잘 표현하기 때문에(로봇팔의 4-5-6축이 마치 zyz축과 유사한 경우가 많다) 로보틱스 같은 분야에서 많이 사용된다.

또 한 가지 재미있는 사실은 앞서 roll-pitch-yaw에서 언급했던 것처럼 intrinsic과 extrinsic rotation의 적용 순서를 반대로 하면 같은 결과를 준다는 점이다. 아래의 예시를 한 번 보자.

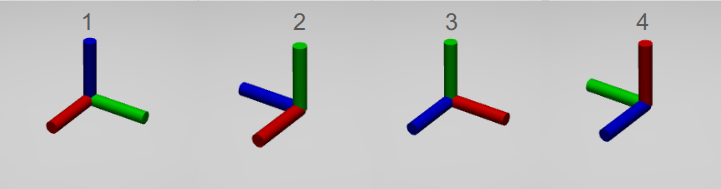
위 그림은 intrinsic rotation으로 xyz 순서로 90도씩 회전한 결과이다. 아래 그림은 extrinsic rotation으로 zyx 순서로 90도씩 회전한 결과이다. 우측 상단에 fixed frame을 함께 표현했다.

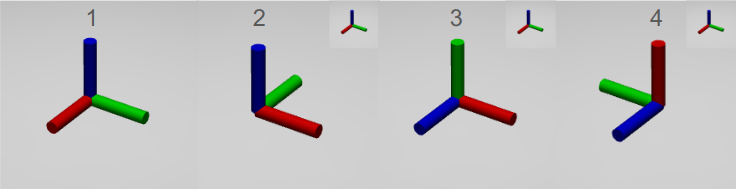
두 그림을 비교해보면 최종적으로 회전한 결과(4)는 같다는 것을 확인할 수 있다.

Rotation matrix

Rotation matrix는 Euler angle의 개념을 행렬의 형태로 표현한 것이라고 할 수 있겠다. 먼저 이해를 비교적 이해하기 쉬운 2차원에서 rotation matrix를 살펴보자.

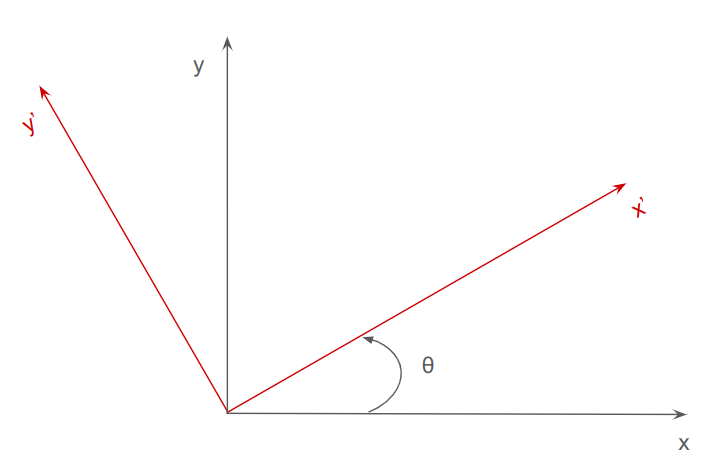
rotation matrix는 아래와 같이 표현된다.

\[\begin{align}R(\theta) &= \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}\\ \begin{bmatrix} x' \\ y' \end{bmatrix} &= \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\end{align}\]

여기서 \(x', y'\)은 회전 후의 좌표이고, \(x, y\)는 회전 전의 좌표이다. 이를 확인해보기 위해 x축 방향의 단위 벡터(1,0)와 y축 방향의 단위 벡터(0,1)을 각각 \(\theta\)만큼 회전해 보자. 2차원에서의 회전은 matrix 계산을 하지 않고, 삼각함수로 쉽게 계산할 수 있으니, 먼저 삼각함수로 계산을 해본 뒤 아래 결과와 비교해 볼 것을 권장한다.

\[\begin{align}\begin{bmatrix} cos(\theta) \\ sin(\theta) \end{bmatrix} &= \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\\ \begin{bmatrix} -sin(\theta) \\ cos(\theta) \end{bmatrix} &= \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}\end{align}\]

직접 삼각함수를 이용해서 계산을 한 것과 같은 결과가 나오는 것을 확인할 수 있다. 여기서 한 가지 재미있는 점은 rotation matrix의 첫 번째 열(column)은 x축 방향의 단위 벡터를 회전한 결과와 같고, 두 번째 열은 y축 방향의 단위 벡터를 회전한 결과와 같다는 것이다. 이 사실은 종종 rotation matrix를 계산할 때 유용하게 쓰인다.

이제 rotation matrix를 3차원으로 확장해보자. 앞서 언급했던 것처럼 rotation matrix는 Euler angle의 개념을 수학적으로 표현한 것이기 때문에 Euler angle에서처럼 각 축의 회전을 순차적으로 적용해주면 된다. 아래의 수식은 xyz 축으로의 회전을 모두 곱하여 3차원 rotation matrix를 얻어내는 과정이다.

\[\begin{align}R &= R_z(\gamma)R_y(\beta)R_x(\alpha)\\ &= \begin{bmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos(\beta) & 0 & sin(\beta) \\ 0 & 1 & 0 \\ -sin(\beta) & 0 & cos(\beta) \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \end{bmatrix}\\ &= \begin{bmatrix} cos(\beta)cos(\gamma) & sin(\alpha)sin(\beta)cos(\gamma)-cos(\alpha)sin(\gamma) & cos(\alpha)sin(\beta)cos(\gamma)+sin(\alpha)sin(\gamma) \\ cos(\beta)sin(\gamma) & sin(\alpha)sin(\beta)sin(\gamma)+cos(\alpha)cos(\gamma) & cos(\alpha)sin(\beta)sin(\gamma)-sin(\alpha)cos(\gamma) \\ -sin(\beta) & sin(\alpha)cos(\beta) & cos(\alpha)cos(\beta) \end{bmatrix}\end{align}\]

여기에서도 2차원에서와 마찬가지로 첫 번째 열은 x축 방향의 단위 벡터를 회전한 결과와 같고, 두 번째, 세 번째 열은 각각 y, z축 방향의 단위 벡터를 회전한 결과와 같다.

그렇다면 위 수식의 회전 적용 순서는 어떻게 되는 것일까? \(R_z\)가 가장 먼저 적혀져 있기 때문에 z축 회전이 먼저 적용되는 것일까? 아니면 \(R_x\)가 가장 먼저 회전하고자 하는 좌표와 곱해지기 때문에 x축 회전이 먼저 적용되는 것일까?

정답은 관점에 따라 다르다이다. 각 축의 rotation matrix는 고정 좌표계를 기준으로 작성된 것이므로, \(R_x\)가 가장 먼저 곱해지는 것은 extrinsic rotation의 관점으로 해석하는 것이고, 즉, 이는 xyz 순서로 회전을 적용하는 것과 같다. 그리고 앞서 살펴봤던 것처럼 이것은 intrinsic rotation으로는 zyx 순서와 같다. 따라서 위 수식은 Euler-xyz(extrinsic)와 같고, 이는 roll-pitch-yaw 방식과 같기도 하다.

Axis-angle

다음으로 살펴볼 각도 표기법은 axis-angle 이라고 하는 표기법이다. 이전까지는 모두 회전을 3개의 축(x,y,z)으로 나누어서 생각했다면 axis-angle은 이름 그대로, 회전 축과 회전 각도를 통해 회전을 나타내는 방법이다. 즉, 이전의 방법들과는 달리, x,y,z 축을 기준으로 회전하는 것이 아니라 임의의 축을 기준으로 회전하는 것이다. 아래 그림에서처럼 회전축의 단위 벡터(\(\overrightarrow{u}\))와 회전 각도(\(\theta\))로 3차원 회전을 표현할 수 있다.

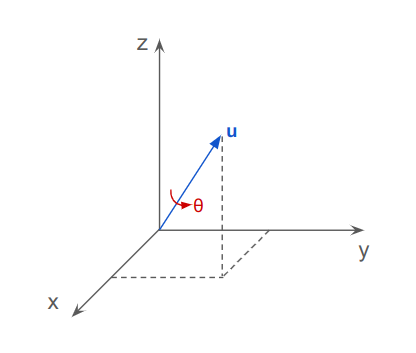
여기서 한 가지 의문이 드는 것은 과연 모든 회전(앞서 살펴봤던 것처럼 3개의 회전축으로 모두 회전하는 경우)을 하나의 축에 대한 회전으로 바꿀 수 있는가 하는 점이다. 이것은 Euler’s rotation theorem에 의해 증명된 것인데 답은 그렇다이다. 즉, 어떠한 회전이라도 하나의 축과 그 축에 대한 회전으로 표현할 수 있다.

Quaternion

마지막으로 살펴볼 방법은 quaternion이다. Quaternion은 계산하는 방법을 아는 것은 어렵지 않지만, 그 개념을 이해하는 것은 꽤나 까다롭다.

먼저, quaternion을 본격적으로 살펴보기 전에 complex plane에 대한 이해가 필요하다. 아래 그림과 같이 x축을 실수(real number)축, y축을 허수(imaginary number)축이라고 정의하면 \(2+i\)와 같은 복소수(complex number)는 \((2,1)\) 지점에 표시할 수 있게 된다.

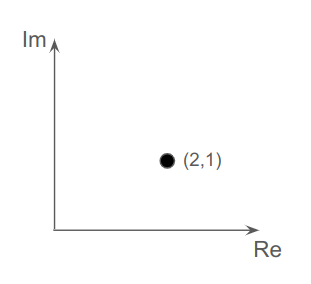
여기서 \(2+i\)에 \(i\)를 곱하게 되면 \(2i-1\)이 되는데, 이는 재미있게도 \((2,1)\)을 시계방향으로 90도 회전한 결과\((-1,2)\)와 일치하게 된다. 한 번더 \(i\)를 곱해도 역시 시계방향으로 90도 회전한 결과와 같게 된다. 이를 일반화 해보면 아래와 같다.

\[x=a+bi,\ r=cos(\theta) + sin(\theta)i \ \text{일 때,}\\ xr = acos(\theta)-bsin(\theta) + (asin(\theta)+bcos(\theta))i\]

위의 식을 보면, 앞서 살펴봤던 2차원 rotation matrix를 곱한 것과 같은 결과인 것(여기서는 x,y 대신 a,b가 쓰였다)을 확인할 수 있다. 즉, complex plane에서는 회전을 단순히 곱으로 표현할 수 있게 된다.

Quaternion을 고안해낸 수학자 W. R. Hamilton은 이러한 complex plane의 개념을 공간으로 확장하고자 노력했고, 그 결과가 quaternion이라고 할 수 있다. 실수와 허수를 통해 평면을 나타냈으므로, 공간을 나타내기 위해서는 하나의 수의 개념만 더 추가하면 될 것 같지만, 결국 Hamilton이 고안해낸 것은 새로운 3개의 허수를 이용해 공간을 나타내는 것이고, 이 허수들의 특성은 아래의 식으로 표현할 수 있다.

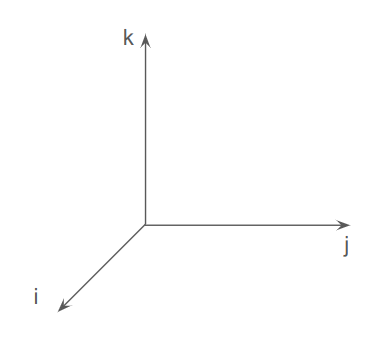
\[\boldsymbol{i}^2=\boldsymbol{j}^2=\boldsymbol{k}^2=\boldsymbol{ijk}=-1 \\ \boldsymbol{ij} = -\boldsymbol{ji} = \boldsymbol{k} \\ \boldsymbol{ki} = -\boldsymbol{ik} = \boldsymbol{j} \\ \boldsymbol{jk} = -\boldsymbol{kj} = \boldsymbol{i} \\\]

기존의 실수와 허수가 아닌 위와 같은 정의를 갖는 새로운 허수(?)를 고안해낸 것이다. 각각의 허수를 하나의 축으로 나타내면 아래와 같이 공간을 표현할 수 있게 된다. 마치 \(ijk\)가 \(xyz\) 축인 것과 유사하다. 위의 식에서 두 개 축의 곱을 회전으로 생각해보면 뒤에 있는 축을 앞에 있는 축을 기준으로 90도 회전한 것이 된다. 즉, \(\boldsymbol{ij}=\boldsymbol{k}\)는 \(j\)축을 \(i\)축을 기준으로 90도 회전하게 되면 \(k\)축이 되는 것으로 생각할 수 있다. 뭔가 2차원에서처럼 곱을 이용해서 회전을 표현할 수 있겠다는 것을 알 수 있다.

본격적으로 회전에 대해서 알아보기 전에 먼저 quaternion에 대한 이해를 해보자. Quaternion을 3개의 허수와 실수를 이용해서 나타내면 다음과 같다.

\[q = q_1 + q_2\boldsymbol{i} + q_3\boldsymbol{j} + q_4\boldsymbol{k}\]

여기서 실수부 즉, \(q_1\)을 스칼라(scalar) 부분이라고 하고, 허수부 즉, \(q_2\boldsymbol{i} + q_3\boldsymbol{j} + q_r\boldsymbol{k}\)을 벡터(vector) 부분이라고 한다. 여기에서는 3개의 허수부만을 이용해 3차원 공간을 나타내고 있기 때문에(\(ijk\)축이 \(xyz\)축과 대응된다), 공간 상의 임의의 벡터를 나타낼 때는 허수부 즉, 벡터 부분만을 이용해서 표시할 수 있고, 이를 pure quaternion이라고 한다. 즉, 위의 정의에서 \(q_1=0\)일 때를 pure quaternion이라고 한다.

🗒 Note! Quaternion은 4차원이므로, 3차원을 나타내기 위해서는 1차원을 제거해야 한다.

quaternion의 연산 방법에 대해서도 간단히 확인해보자. 먼저, 덧셈은 아래와 같은 방법으로 할 수 있다.

\[\begin{align} p+q &= (p_1 + p_2\boldsymbol{i} + p_3\boldsymbol{j} + p_4\boldsymbol{k}) + (q_1 + q_2\boldsymbol{i} + q_3\boldsymbol{j} + q_r\boldsymbol{k}) \\ &= (p_1+q_1) + (p_2+q_2)\boldsymbol{i} + (p_3+q_3)\boldsymbol{j} + (p_4+q_4)\boldsymbol{k} \end{align}\]

곱셉은 아래와 같이 계산할 수 있다.

\[\begin{align} pq &= (p_1 + p_2\boldsymbol{i} + p_3\boldsymbol{j} + p_4\boldsymbol{k})(q_1 + q_2\boldsymbol{i} + q_3\boldsymbol{j} + q_r\boldsymbol{k}) \\ &= (p_1q_1-p_2q_2-p_3q_3-p_4q_4) + (p_1q_2+p_2q_1+p_3q_4-p_4q_3)\boldsymbol{i} \\ &\quad + (p_1q_3+p_3q_1+p_4q_2-p_2q_4)\boldsymbol{j} + (p_1q_4+p_4q_1+p_2q_3-p_3q_2)\boldsymbol{k} \end{align}\]

곱셉의 계산식을 조금 다르게 나타내면 아래와 같이 나타낼 수도 있다.

\[\begin{align} pq &= (p_1q_1-p_2q_2-p_3q_3-p_4q_4)\\ &\quad + p_1(q_2\boldsymbol{i}+q_3\boldsymbol{j}+q_4\boldsymbol{k}) + q_1(p_2\boldsymbol{i}+p_3\boldsymbol{j}+p_4\boldsymbol{k})\\ &\quad + (p_3q_4-p_4q_3)\boldsymbol{i} + (p_4q_2-p_2q_4)\boldsymbol{j} + (p_2q_3-p_3q_2)\boldsymbol{k} \\ & = p_1q_1 - \boldsymbol{v_p}\cdot\boldsymbol{v_q} + p_1\boldsymbol{v_q} + q_1\boldsymbol{v_p} + \boldsymbol{v_p} \times \boldsymbol{v_q}\end{align}\] \[\begin{align}\text{where} & \\ &\boldsymbol{v_p} = p_2\boldsymbol{i} + p_3\boldsymbol{j} + p_4\boldsymbol{k} \\ &\boldsymbol{v_q} = q_2\boldsymbol{i} + q_3\boldsymbol{j} + q_4\boldsymbol{k}\end{align}\]

여기서 quaternion의 허수부를 마치 우리가 기존에 알고 있던 벡터로 생각해서 식을 변환한 것이다. 내적(dot product)과 외적(cross product)은 일반적인 벡터의 연산을 나타낸다.

켤레 복소수(conjugate)는 아래와 같이 나타낼 수 있다.

\[\overline{q} = q_1 - q_2\boldsymbol{i} - q_3\boldsymbol{j} - q_4\boldsymbol{k}\]

이제 본격적으로 quaternion으로 어떻게 회전을 표현할 수 있는지 살펴보자. 먼저, 공간상의 벡터 \(x\)와 회전 \(r\)을 다음과 같이 정의하자. 벡터는 3차원의 개념이므로 pure quaternion으로, 회전은 스칼라 부분을 갖는 quaternion으로 정의한다.

\[\begin{align} x&=x_2\boldsymbol{i}+x_3\boldsymbol{j}+x_4\boldsymbol{k} = \boldsymbol{v_x} \\ r&=r_1+r_2\boldsymbol{i}+r_3\boldsymbol{i}+r_4\boldsymbol{j}=r_1+\boldsymbol{v_r} \end{align}\]

2차원에서 회전을 적용했던 것처럼 \(x\)와 \(r\)을 곱해보자. 여기에서는 곱의 순서가 중요하기 때문에(\(\boldsymbol{ij} \not= \boldsymbol{jk}\)) 계산 순서에 주의가 필요하다.

\[rx = -\boldsymbol{v_r} \cdot \boldsymbol{v_x} + r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x}\]

계산의 편의를 위해 \(\boldsymbol{v_r} \cdot \boldsymbol{v_x} = 0\) 인 경우를 예로 들어보자. 벡터의 내적은 서로 수직일 때 0이 되므로, \(\boldsymbol{v_x} = v_x\boldsymbol{i}\), \(\boldsymbol{v_r} = v_r\boldsymbol{j}\) 인 경우에 계산을 해보면 다음과 같다.

\[\begin{align} rx &= r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x} \\ &= r_1v_x\boldsymbol{i} - v_rv_x\boldsymbol{k} \\ &= v_x(r_1\boldsymbol{i} - v_r\boldsymbol{k})\end{align}\]

그런데 \(v_x\boldsymbol{i}\)(크기가 \(v_x\)인 \(i\) 방향 벡터)를 \(j\) 축을 기준으로 회전시키는 경우를 생각해보면 그 결과가 \(v_x(cos(\theta)\boldsymbol{i} - sin(\theta)\boldsymbol{k})\)가 되는 것을 알 수 있다. 이를 위의 결과와 비교해보면, \(r_1 = cos(\theta)\), \(v_r = sin(\theta)\)로 치환하면 회전시킨 것과 결과가 같다는 것을 알 수 있다. 즉, 특정한 형태의 quaternion을 이용하면 회전을 표현할 수 있는 것이다. 이를 토대로 단위 벡터 \(\overrightarrow{u}\)를 축으로 \(\theta\)만큼 회전하는 것을 quaternion으로 나타내면 다음과 같이 나타낼 수 있을 것이다(뒤\(\eqref{eq2}\)에서 추가적으로 설명을 하겠지만 사실 이 수식은 틀린 수식이다).

\[q = cos(\theta)+sin(\theta)\boldsymbol{u} \tag{1} \label{eq1}\]

🗒 Note! 회전 축과 각도로 회전을 나타낸다는 점에서 axis-angle의 개념과 유사하다. 축(3차원)과 각도(1차원)로 표현하는 것이기 때문에 회전은 4차원의 개념이다.

그렇다면 이제 \(\boldsymbol{v_r} \cdot \boldsymbol{v_x} \not= 0\) 인 경우를 살펴보자. \(\boldsymbol{v_x} = v_{xi}\boldsymbol{i} + v_{xj}\boldsymbol{j}\), \(\boldsymbol{v_r} = v_r\boldsymbol{j}\) 인 경우는 아래와 같이 계산할 수 있다.

\[\begin{align} rx &= -\boldsymbol{v_r} \cdot \boldsymbol{v_x} + r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x} \\ &= -v_{xj}v_r + r_1v_{xi}\boldsymbol{i} + r_1v_{xj}\boldsymbol{j} - v_rv_{xi}\boldsymbol{k} \\ \\ &\text{여기서} \ r_1 = cos(\theta), \ v_r = sin(\theta) \ \text{이면,} \\ rx &= -v_{xj}sin(\theta) + cos(\theta)v_{xi}\boldsymbol{i} + cos(\theta)v_{xj}\boldsymbol{j} - sin(\theta)v_{xi}\boldsymbol{k} \end{align}\]

이 경우에는 회전의 결과가 pure quaternion이 아니다. 즉, 3차원 벡터를 회전한 결과가 4차원의 어떤 값으로 나타나게 된다. 또한, 벡터의 크기가 보존되었던 이전 결과와는 달리 이 경우에는 벡터의 크기가 보존되지 않는 것을 확인할 수 있다(\(v_{xi}^2 + v_{xj}^2 \not= v_{xi}^2 + cos(\theta)^2v_{xj}^2\)). 물론 quaternion의 크기로 생각해도 크기가 보존되지 않는다.

결과를 정리해보면, \(\boldsymbol{v_r} \cdot \boldsymbol{v_x} = 0\) 인 경우에는 quaternion의 곱을 이용해 회전을 표현하는 것이 가능한 것처럼 보였으나, 이 결과를 \(\boldsymbol{v_r} \cdot \boldsymbol{v_x} \not= 0\) 인 경우로까지 확장할 수는 없었다.

그런데 아주 재미있게도 Hamilton은 켤레 복소수를 이용하면 위의 문제를 해결할 수 있음을 발견해냈다. \(\bar{r} = r_1 - \boldsymbol{v_r}\) 이라 하면

\[\begin{align} rx\bar{r} &= (-\boldsymbol{v_r}\cdot\boldsymbol{v_x} + r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x})(r_1 - \boldsymbol{v_r}) \\ &= -r_1\boldsymbol{v_r} \cdot \boldsymbol{v_x} + (r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x})\cdot\boldsymbol{v_r} \\ &\quad + (\boldsymbol{v_r}\cdot\boldsymbol{v_x})\boldsymbol{v_r} + r_1(r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x}) \\ &\quad - (r_1\boldsymbol{v_x} + \boldsymbol{v_r} \times \boldsymbol{v_x})\times\boldsymbol{v_r} \\ &= (\boldsymbol{v_r}\cdot\boldsymbol{v_x})\boldsymbol{v_r} + r_1^2\boldsymbol{v_x} + 2r_1\boldsymbol{v_r} \times \boldsymbol{v_x} - (\boldsymbol{v_r} \times \boldsymbol{v_x})\times \boldsymbol{v_r} \end{align}\]

이 되고, \(\boldsymbol{v_x} = v_{xi}\boldsymbol{i} + v_{xj}\boldsymbol{j}\), \(\boldsymbol{v_r} = v_r\boldsymbol{j}\) 를 대입하면

\[\begin{align} rx\bar{r} &= v_{xj}v_r^2\boldsymbol{j} + r_1^2(v_{xi}\boldsymbol{i} + v_{xj}\boldsymbol{j}) +2r_1(-v_rv_{xi}\boldsymbol{k}) + v_rv_{xi}\boldsymbol{k} \times v_r\boldsymbol{j} \\ &= (r_1^2 - v_r^2)v_{xi}\boldsymbol{i} + (r_1^2 + v_r^2)v_{xj}\boldsymbol{j} -2r_1v_rv_{xi}\boldsymbol{k} \end{align}\]

이 된다. 여기서는 결과가 pure quaternion이고, 벡터의 크기 또한 보존되는 것을 확인할 수 있다. 실제로 값을 대입해서 회전의 결과도 한 번 살펴보자. \(v_{xi} = \frac{\sqrt{2}}{2}\), \(v_{xj} = \frac{\sqrt{2}}{2}\), \(r_1 = cos(90°)\), \(v_r = sin(90°)\) 로 치환 후 계산을 해보면

\[\begin{align} rx\bar{r} &= -\frac{\sqrt{2}}{2}\boldsymbol{i} + \frac{\sqrt{2}}{2}\boldsymbol{j} \end{align}\]

이 된다. 벡터 \((\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}, 0)\)를 y축으로 90도 회전 시킨 결과는 \((0, \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})\)가 되어야 하는데 예상과는 다른 결과가 나온 것을 확인할 수 있다. 그런데 결과를 자세히 보면 완전히 다른 결과가 나온 것은 아니고, y축을 기준으로 180도 회전 시킨 결과인 것을 알 수 있다.

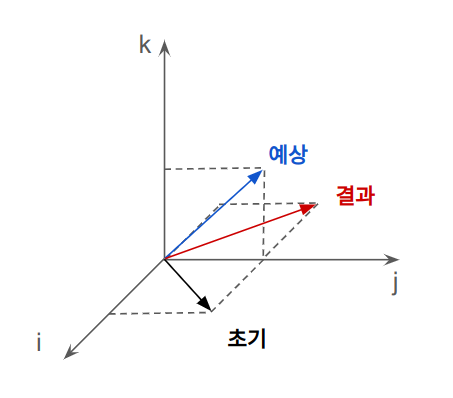
예상했던 회전의 두 배만큼 회전한 결과인 것이다. 이는 회전을 2번 적용한 것이라고 이해할 수 있을 것 같다. 즉, quaternion을 통해 회전을 나타내려고 했더니 회전을 한 번 곱하는 것으로는 원하는 결과를 얻지 못했고(차원과 크기가 보존되지 않음), 이를 해결하기 위해 회전을 한 번 더 곱해주었더니(켤레 복소수를 곱함), 그 결과 차원과 크기는 보존되었지만 회전 각도가 2배가 된 것이다.

이를 토대로 진짜 회전 quaternion을 수식(앞서 언급했던 것처럼 \(\eqref{eq1}\)은 틀린 식이다)으로 나타내면 다음과 같다.

\[q = cos(\frac{\theta}{2})+sin(\frac{\theta}{2})\boldsymbol{u} \tag{2} \label{eq2}\]

그리고 앞서 살펴봤던 것처럼 벡터(pure quaternion) \(p\)를 회전하기 위해서는 \(qp\bar{q}\) 와 같이 계산할 수 있다.

그렇다면 이렇게나 이해하기 어렵고, 직관적이지 않은 quaternion을 왜 사용하는 것일까?

quaternion은 하나의 회전에 대해서 단 하나의 값만을 가지는 장점이 있다. 이전에 살펴봤던 모든 방법들은 하나의 회전에 대한 표현 방법이 유일하지 않다. 즉, 같은 회전 결과를 표현할 수 있는 방법이 여러가지가 존재한다. 이러한 quaternion의 유일성은 각도를 비교하거나 각도차를 계산할 때 유용하게 활용된다.

ℹ Info! Intrinsic rotation으로 y축으로 90도, x축으로 90도를 순서대로 회전한 결과와 z축으로 -90도, y축으로 90도 순서대로 회전한 결과는 같다.

이는 다른 표현으로는 gimbal lock을 피할 수 있다라고도 할 수 있다. Gimbal lock이란 3차원에서 회전을 표현할 때, 특정한 경우에 회전 자유도를 잃게되는 것이다. 앞서 살펴봤던 rotation matrix를 \(\beta = \frac{\pi}{2}\) 인 경우로 계산해보면

\[\begin{align}R &= \begin{bmatrix} 0 & sin(\alpha)cos(\gamma)-cos(\alpha)sin(\gamma) & cos(\alpha)cos(\gamma)+sin(\alpha)sin(\gamma) \\ 0 & sin(\alpha)sin(\gamma)+cos(\alpha)cos(\gamma) & cos(\alpha)sin(\gamma)-sin(\alpha)cos(\gamma) \\ -1 & 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} 0 & sin(\alpha-\gamma) & cos(\alpha-\gamma) \\ 0 & cos(\alpha-\gamma) & -sin(\alpha-\gamma) \\ -1 & 0 & 0 \end{bmatrix} \end{align}\]

이 된다. 이 경우 \(\alpha\) 또는 \(\gamma\)의 값을 변경하는 것이 같은 결과를 가져온다. 2개의 값으로 1개의 자유도만 표현이 가능한 것이다. 즉, x축으로의 회전은 z축으로의 회전으로도 표현할 수 있고, 이는 비유일성을 나타낸다.

🗒 Note! 여기서 주의할 점은 gimbal lock은 물리적 현상이 아니라는 점이다. 즉, 실제로 물체가 특정 방향으로 회전을 할 수 없는 것은 아니다. 이는 gimbal에서만 물리적으로 나타나는 현상이고, 따라서 gimbal lock이라는 이름이 붙은 것이다.